Experiência que necessitará de um celular ou computadores com acesso digital.










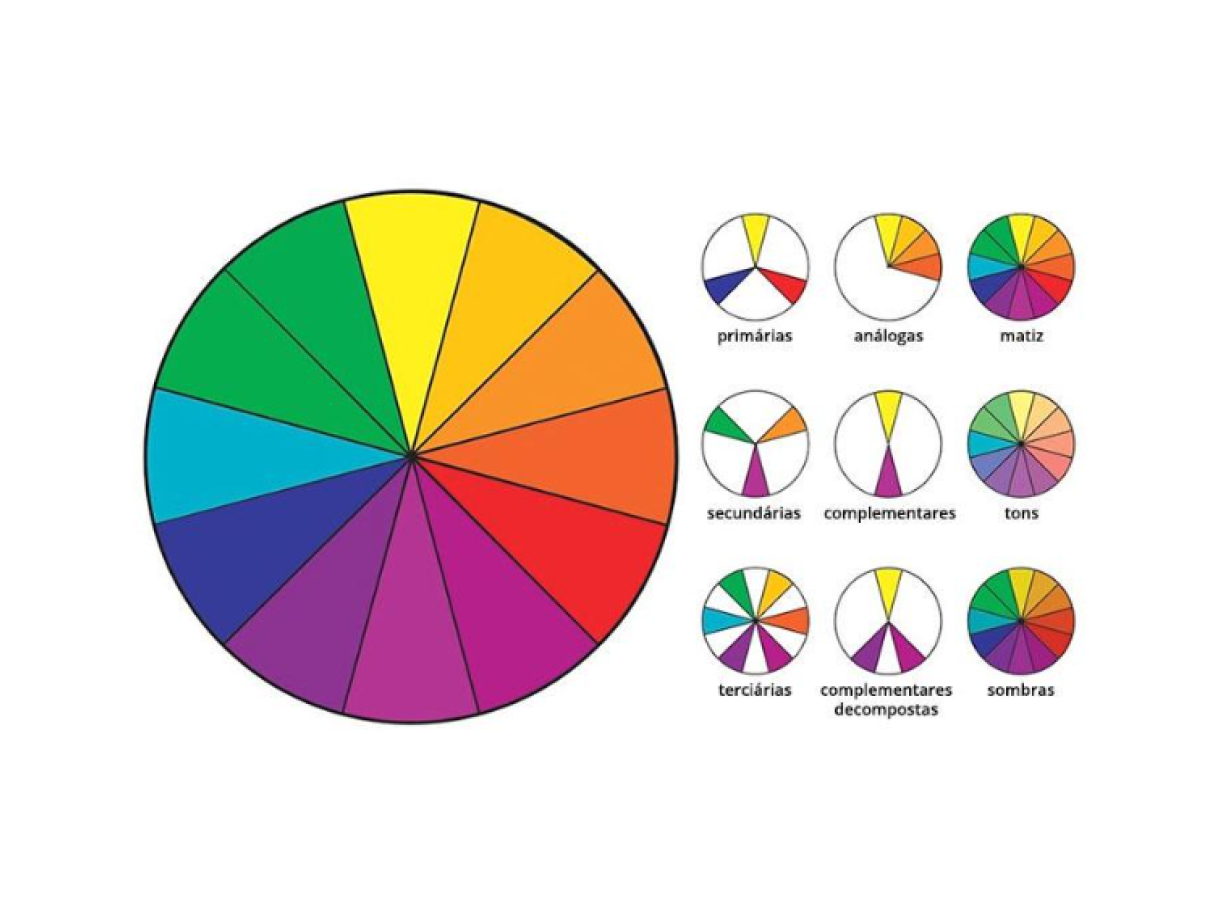
Para iniciar o estudo, pesquisem a teoria das cores.
Proponha para a turma o seguinte experimento preparatório: durante alguns minutos, sob boa luz, olhe diretamente para uma cor, por exemplo, amarelo. Depois olhe para uma superfície branca, e perceba que uma outra cor aparece: violeta. Violeta é complementar ao amarelo.
Cores complementares são as que estão opostas no disco das cores.
Explore e questione a partir da imagem do Disco de Newton.
O Disco de Newton é um experimento muito conhecido da Física. Consiste em um disco colorido com as cores primárias do espectro visível (vermelho, laranja, amarelo, verde, azul, anil e violeta). Esse disco gira, apresenta grande velocidade e tem como objetivo mostrar a composição da luz branca.
Quando parado, a separação das cores é nítida, no entanto, ao colocarmos o disco para girar, as cores misturam-se, e o disco parece ficar branco. Newton fez uso desse dispositivo para identificar que a mistura das cores visíveis produzia a cor branca.
Para mais informações, acesse:
Experimento do disco de Newton – Educador Brasil Escola
Artes:
Descubra com os educandos as cores que ficam harmoniosas em cada diferente cor de pele. Isso se chama Colorimetria.
Dá uma olhada nesse material de consulta:
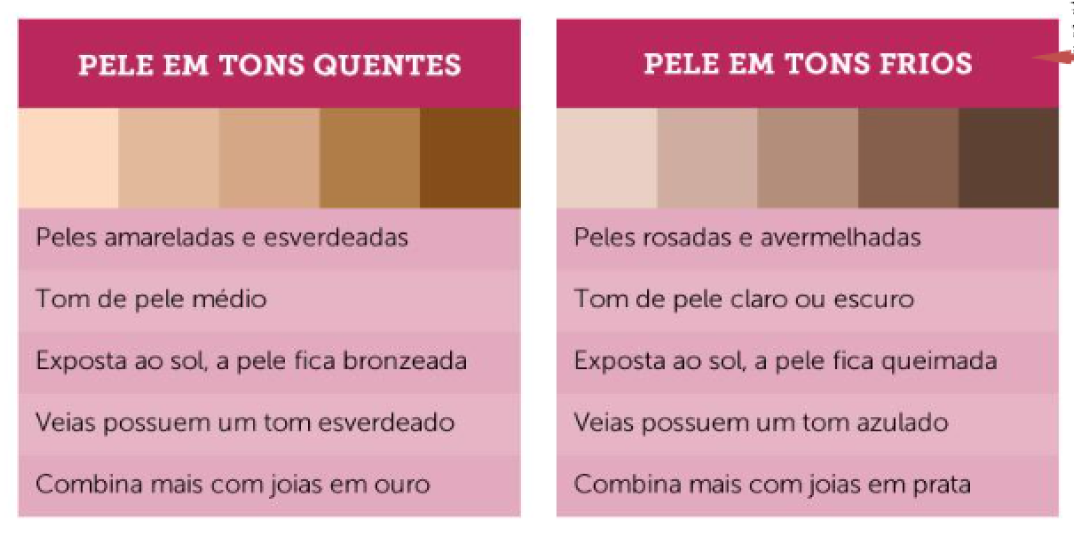

Como saber a Colorimetria?
De acordo com seu tipo de pele (em tons quentes ou frios), você irá descobrir qual mais se assemelha às que estão nas paletas da Colorimetria: primavera, verão, outono ou inverno.

Matemática:
Sugere-se trabalhar com frações e proporções. Você pode estudar o conceito de frações perguntando:
Qual a fração do disco que cada cor representa? (1/7 para cada cor). E peça que escrevam as frações em cada segmento do disco.
Outra boa ideia é falar sobre a relação entre a arte e a matemática. Dá só uma conferida em alguns exemplos de artistas que usam a matemática como recurso em seus trabalhos:
M.C. Escher é conhecido por explorar perspectivas e simetria. Obras como “Relativity” e “Metamorphosis I, II e III” exemplificam essa relação entre matemática e arte.
O uso da proporção áurea é comum em obras de artistas como Leonardo da Vinci. O “Homem Vitruviano” é um exemplo perfeito de como a proporção e a simetria são integradas à forma humana.
Artistas contemporâneos, como Olafur Eliasson, usam padrões geométricos e princípios matemáticos em suas instalações, criando experiências visuais que fazem os espectadores refletirem sobre a relação entre matemática e natureza.
Confira: Your ocular relief: Olafur Eliasson’s Ethereal Light Show
DICA:
Você pode ainda criar desenhos utilizando régua e compasso, como mandalas ou padrões geométricos, uma maneira divertida de explorar a conexão entre matemática e arte.
Português e história:
Proponha pesquisar sobre a biografia de Isaac Newton.
Nesta etapa, você e seus educandos irão aplicar o método com o passo a passo, seguindo as orientações e a metodologia indicada. Um ótimo experimento para você e os seus educandos!
Com o compasso, façam um círculo, tendo por base o tamanho de um CD.
Com a régua e o lápis, façam divisões triangulares no círculo, todas com o mesmo tamanho, como uma pizza.
Pintem os triângulos e certifiquem-se de deixar todos os espaços totalmente coloridos e sem falhas.
Façam um pequeno furo circular no centro do círculo com o furador de papel. Pelo furo, passe um lápis e faça um apoio, enrolando o lápis com a fita do lado da parte branca da cartolina.
Agora é só garantir a rotação do disco. Quanto mais rápido o disco girar, maior será o efeito da composição da luz branca sobre os nossos olhos.
Busque jogos em que seus educandos possam aprofundar seus estudos sobre as cores, em especial, jogos que estimulem a percepção de como as cores estão relacionadas com a natureza e conosco, seres humanos.
É o uso de elementos e mecânicas de jogos para engajar os alunos no processo de aprendizagem. Isso envolve a aplicação de desafios, recompensas, competições e narrativas no contexto educacional ou corporativo, para tornar o aprendizado mais dinâmico, motivador e eficaz.
A estratégia é aplicada por professores que incorporam elementos de jogos, como pontos, níveis, medalhas ou rankings. Esses elementos são projetados para motivar os alunos, promover a colaboração, estimular a resolução de problemas e recompensar o progresso.
Para concluir esse experimento, proponha um estudo individual de Colorimetria de cada educando. Sugira a seus educandos que realizem em casa esse estudo ampliando para outros membros da família. Peça que registrem a experiência com fotos.
